Sistem Bilangan

Sistem Bilangan

Sistem Bilangan atau Number System adalah Suatu cara untuk mewakili besaran dari suatu item fisik. Sistem Bilangan menggunakan suatu bilangan dasar atau basis (base / radix) yang tertentu. Dalam hubungannya dengan komputer, ada 4 Jenis Sistem Bilangan yang dikenal yaitu : Desimal (Basis 10), Biner (Basis 2), Oktal (Basis 8) dan Hexadesimal (Basis 16).

Penerapan Sistem Bilangan

Komputer menggunakan beberapa jenis bilangan. Contoh penggunaan sistem bilangan pada komputer adalah :

1. Bilangan Biner. Bilangan ini adalah bilangan dasar yang digunakan komputer
2. Bilangan Desimal. Bilangan ini dapat kita jumpai pada pengalamatan IP dalam jaringan komputer 
3. Bilangan Heksadesimal. Bilangan ini dapat kita jumpai pada MAC Address setiap device.

Penerapan bilangan Heksadesimal dan Desimal

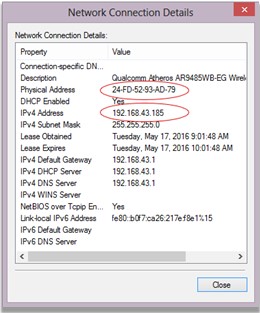Contoh penerapan bilangan Heksadesimal dan Desimal

Jenis-Jenis Bilangan

1. Bilangan Biner. Bilangan ini hanya mengenal dua jenis angka numerik, yaitu 0 dan 1. Nilai 1 mewakili keadaan dengan arus listrik, sementara nilai 0 mewakili keadaan sebaliknya. Penulisan bilangan biner menggunakan format N2.
2. Bilangan Oktal adalah bilangan yang menggunakan 8 jenis angka numerik, yaitu 0,1,2,3,4,5,6, dan 7.
3. Bilangan Heksadesimal terdiri dari 10 angka numerik, yaitu 0 hingga 9, dan 6 karakter, yaitu A, B, C, D, E, F. nilai A mewakili nilai 10, B mewakili nilai 11, dan seterusnya.

Konversi Bilangan

Konversi adalah teknik mengubah suatu bentuk menjadi bentuk lainnya, tetapi tetap memiliki arti yang sama. Sebagai contoh, konversi bilangan desimal menjadi bilangan biner sangatlah penting ketika menghitung banyaknya network yang terbentuk dari subnetting IP Address. Terdapat beberapa teknik konversi bilangan, yaitu menjumlahkan suku bilangan yang dikonversi, atau melakukan pembagian bilangan secara berulang.

• Cara Konversi Bilangan Biner

Berikut adalah cara mengonversi bilangan biner bulat menjadi format desimal dengan cara mengalikan setiap suku bilangan sesuai dengan urutan pangkatnya :

11102 = (1x23) + (1x22) + (1x21) + (0x20)

           = 8 + 4 + 2 + 0                                     = 1410

Sedangkan cara mengonversi bilangan biner dengan angka di belakang koma adalah :

1,111 2  = (1x20) + (1x2-1) + (1x2-2) + (1x2-3)

               = 1 + 0,5 + 0,25 + 0,125                   = 1,87510

• Cara Konversi Bilangan Oktal

Cara mengonversi bilangan Oktal menjadi format desimal adalah :

3218 = (3x82) + (2x81) + (1x80)

          = 192 + 16 + 1                                         = 20910

Sedangkan cara mengonversi bilangan Oktal dengan angka di belakang koma adalah :

31,22 8  = (3x81) + (1x80) + (2x8-1) + (2x8-2)

               = 24 + 1 + 0,25 + 0,0312                   = 25,28128

• Cara Konversi Bilangan Heksadesimal

Cara mengonversi bilangan heksadesimal bulat menjadi format desimal adalah :

A1216 = (10x162) + (1x161) + (2x160)

            = 2560 + 16 + 2                                      = 257810

Sedangkan cara mengonversi bilangan heksadesimal dengan angka di belakang koma adalah :

A12,2116  = (10x162) + (1x161) + (2x160) + (2x16-1) + (1x16-2)

       = 2560 + 16 + 2 + 0,125 + 0,00391

       = 2578,1289110 

Konversi Bilangan Dengan Pembagian Berulang

Teknik konversi bilangan lainnya adalah pembagian secara berulang. Bilangan awal yang akan dikonversi dibagi dengan basis bilangan hasilnya. Sebagai contoh, bilangan Oktal yang akan dikonversi menjadi desimal dibagi dengan angka 10.

Contoh Konversi Bilangan Desimal 

Konversikan bilangan 19210  menjadi bilangan berbasis biner.

Penulisan hasil konversi bilangan 19210 ke dalam bentuk biner adalah menuliskan sisa hasil bagi dari bawah ke atas, sehingga diperoleh hasil
 11000000 2. Jadi, 19210 = 11000000 2.

Konversikan bilangan 20010 menjadi bilangan berbasis oktal.

Penulisan hasil konversi bilangan 20010 ke dalam bentuk biner adalah menuliskan sisa hasil bagi dari bawah ke atas, sehingga diperoleh hasil 3108. Jadi, 20010 = 3108.

Sistem Penyandian Bilangan

Komputer hanya mengenali bilangan biner, sehingga ketika user mengetikkan angka 8 pada keyboard, angka tersebut harus di-encode ke dalam bilangan biner untuk kemudian diproses oleh CPU.

CPU kemudian akan mengolah dan mengirimkan data dalam bentuk biner yang kemudian di-encode kembali menjadi desimal untuk ditampilkan di layar komputer. Terdapat beberapa bentuk bilangan yang disandikan, di antaranya adalah.

• Binary Coded Decimal

Pada sistem penyandian BCD, setiap bilangan akan diuraikan dan disandikan berdasarkan sistem biner. Dibutuhkan 4 bit biner untuk menyajikan setiap digit bilangan desimal. Perhatikan contoh berikut :

Binary Coded Decimal  

• Binary Coded Hexadecimal

Sistem sandi BCH digunakan untuk menyajikan data Heksadesimal dalam bentuk biner. Sama seperti BCD, setiap digit bilangan akan diubah dalam kelompok yang terdiri atas kombinasi biner sebanyak 4 bit. Perhatikan tabel kode BCH di samping.

Binary Code Heksadesimal 

ASCII

ASCII (American Standard Code for Information Interchange) merupakan standar yang digunakan pada industry untuk pengkodean huruf, angka, dan karakter-karakter lain dengan menggunakan 128 kode (7 bit). Contoh penggunaan ASCII adalah tombol keyboard komputer. Fungsi tombol-tombol keyboard dibagi menjadi dua, yaitu numerik dan non numerik. Sandi pada tombol yang terdiri atas angka, huruf, dan simbol tertentu disebut sebagai alphanumeric atau alphabet and numeric.

Tabel ASCII